Examples

In the following a few code-snippets are shown which should help you getting started with xrayutilities. Not all of the codes shown in the following will be run-able as stand-alone script. For fully running scripts look in the GitHub examples or in the download.

Reading data from data files

The io submodule provides classes for reading x-ray diffraction data in various formats. In the following few examples are given.

Reading SPEC files

Working with spec files in xrayutilities can be done in two distinct ways.

1. parsing the spec file for scan headers; and parsing the data only when needed

2. parsing the spec file for scan headers; parsing all data and dump them to an HDF5 file; reading the data from the HDF5 file.

Both methods have their pros and cons. For example when you parse the spec-files over a network connection you need to re-read the data again over the network if using method 1) whereas you can dump them to a local file with method 2). But you will parse data of the complete file while dumping it to the HDF5 file.

Both methods work incremental, so they do not start at the beginning of the file when you reread it, but start from the last position they were reading and work with files including data from linear detectors.

An working example for both methods is given in the following.

import xrayutilities as xu
import os

# open spec file or use open SPECfile instance
try: s
except NameError:
    s = xu.io.SPECFile("sample_name.spec", path="./specdir")

# method (1)
s.scan10.ReadData()
scan10data = s.scan10.data

# method (2)
h5file = os.path.join("h5dir", "h5file.h5")
s.Save2HDF5(h5file) # save content of SPEC file to HDF5 file
# read data from HDF5 file
[angle1, angle2], scan10data = xu.io.geth5_scan(h5file, [10],
                                                "motorname1",
                                                "motorname2")

See also

the fully working example hello world

In the following it is shown how to re-parsing the SPEC file for new scans and reread the scans (1) or update the HDF5 file(2)

s.Update() # reparse for new scans in open SPECFile instance

# reread data method (1)
s.scan10.ReadData()
scan10data = s.scan10.data

# reread data method (2)
s.Save2HDF5(h5) # save content of SPEC file to HDF5 file
# read data from HDF5 file
[angle1, angle2], scan10data = xu.io.geth5_scan(h5file, [10],
                                                "motorname1",
                                                "motorname2")

Reading EDF files

EDF files are mostly used to store CCD frames at ESRF recorded from various different detectors. This format is therefore used in combination with SPEC files. In an example the EDFFile class is used to parse the data from EDF files and store them to an HDF5 file. HDF5 if perfectly suited because it can handle large amount of data and compression.

import xrayutilities as xu
import numpy

specfile = "specfile.spec"
h5file = "h5file.h5"

s = xu.io.SPECFile(specfile)
s.Save2HDF5(h5file) # save to hdf5 file

# read ccd frames from EDF files
for i in range(1, 1001, 1):
    efile = "edfdir/sample_%04d.edf" % i
    e = xu.io.edf.EDFFile(efile)
    e.ReadData()
    e.Save2HDF5(h5file, group="/frelon_%04d" % i)

See also

the fully working example provided in the examples directory perfectly suited for reading data from beamline ID01

Reading XRDML files

Files recorded by Panalytical diffractometers in the .xrdml format can be parsed. All supported file formats can also be parsed transparently when they are saved as compressed files using common compression formats. The parsing of such compressed .xrdml files conversion to reciprocal space and visualization by gridding is shown below:

import xrayutilities as xu
om, tt, psd = xu.io.getxrdml_map('rsm_%d.xrdml.bz2', [1, 2, 3, 4, 5],
                                 path='data')
# or using the more flexible function
tt, om, psd = xu.io.getxrdml_scan('rsm_%d.xrdml.bz2', 'Omega',
                                  scannrs=[1, 2, 3, 4, 5], path='data')
# single files can also be opened directly using the low level approach
xf = xu.io.XRDMLFile('data/rsm_1.xrdml.bz2')
# then see xf.scan and its attributes

See also

the fully working example provided in the examples directory

Other formats

Other formats which can be read include

• Rigaku .ras files.

• files produces by the experimental control software at Hasylab/Desy (spectra).

• numor files from the ILL neutron facility

• ccd images in the tiff file format produced by RoperScientific CCD cameras and Perkin Elmer detectors.

• files from recorded by Seifert diffractometer control software (.nja)

• support is also provided for reading of cif files from structure databases to extract unit cell parameters as well es read data from those files (pdCIF, ESG files)

See the examples directory for more information and working example scripts.

Angle calculation using Experiment and materials classes

Methods for high angle x-ray diffraction experiments. Mostly for experiments performed in coplanar scattering geometry. An example will be given for the calculation of the position of Bragg reflections.

>>> import xrayutilities as xu
>>> Si = xu.materials.Si  # load material from materials submodule
>>>
>>> # initialize experimental class with directions from experiment
>>> hxrd = xu.HXRD(Si.Q(1, 1, -2), Si.Q(1, 1, 1))
>>> # calculate angles of Bragg reflections and print them to the screen
>>> om, chi, phi, tt = hxrd.Q2Ang(Si.Q(1, 1, 1))
>>> print("Si (111)")
Si (111)
>>> print(f"om, tt: {om:8.3f} {tt:8.3f}")
om, tt:   14.221   28.442
>>> om, chi, phi, tt = hxrd.Q2Ang(Si.Q(2, 2, 4))
>>> print("Si (224)")
Si (224)
>>> print(f"om, tt: {om:8.3f} {tt:8.3f}")
om, tt:   63.485   88.028

Note that above the HXRD class is initialized without specifying the energy used in the experiment. It will use the default energy stored in the configuration file, which defaults to CuK-\({\alpha}_1\).

One could also call:

hxrd = xu.HXRD(Si.Q(1, 1, -2), Si.Q(1, 1, 1), en=10000)  # energy in eV

to specify the energy explicitly. The HXRD class by default describes a four-circle goniometer as described in more detail here.

Similar functions exist for other experimental geometries. For grazing incidence diffraction one might use

>>> import xrayutilities as xu
>>> gid = xu.GID(xu.materials.Si.Q(1, -1, 0), xu.materials.Si.Q(0, 0, 1))
>>> # calculate angles and print them to the screen
>>> (alphai, azimuth, tt, beta) = gid.Q2Ang(xu.materials.Si.Q(2, -2, 0))
>>> print(f"azimuth, tt: {azimuth:8.3f} {tt:8.3f}")
azimuth, tt:  113.651   47.302

There is on implementation of a GID 2S+2D diffractometer. Be sure to check if the order of the detector circles fits your goniometer, otherwise define one yourself!

There exists also a powder diffraction class, which is able to convert powder scans from angular to reciprocal space.

import xrayutilities as xu
import numpy
energy = 'CuKa12'
# creating powder experiment
xup = xu.PowderExperiment(en=energy)
theta = numpy.arange(0, 70, 0.01)
q = xup.Ang2Q(theta)

More information about powdered materials can be obtained from the PowderDiffraction class. It contains information about peak positions and intensities

>>> import xrayutilities as xu
>>> print(xu.simpack.PowderDiffraction(xu.materials.In))
Powder diffraction object
-------------------------
Powder-In (a: 3.2523, c: 4.9461, at0_In_2a_occupation: 1, at0_In_2a_biso: 0, volume: 1, )
Lattice:
139 tetragonal I4/mmm: a = 3.2523, b = 3.2523 c= 4.9461
alpha = 90.000, beta = 90.000, gamma = 90.000
Lattice base:
0: In (49) 2a  occ=1.000 b=0.000
Reflection conditions:
 general: hkl: h+k+l=2n, hk0: h+k=2n, 0kl: k+l=2n, hhl: l=2n, 00l: l=2n, h00: h=2n
2a      : None

Reflections:
------------
      h k l     |    tth    |    |Q|    |Int     |   Int (%)
   ---------------------------------------------------------------
      (1, 0, 1)    32.9339      2.312       217.24      100.00
      (0, 0, 2)    36.2964      2.541        41.69       19.19
      (1, 1, 0)    39.1392      2.732        67.54       31.09
     (1, 1, -2)    54.4383      3.731        50.58       23.28
      (2, 0, 0)    56.5486      3.864        22.47       10.34
     (1, 0, -3)    63.1775      4.273        31.82       14.65
      (2, 1, 1)    67.0127      4.503        53.09       24.44
      (2, 0, 2)    69.0720      4.624        24.22       11.15
      (0, 0, 4)    77.0641      5.081         4.43        2.04
      (2, 2, 0)    84.1193      5.464         7.13        3.28
     (2, 1, -3)    89.8592      5.761        24.97       11.49
      (1, 1, 4)    90.0301      5.769        12.44        5.73
      (3, 0, 1)    93.3390      5.933        11.75        5.41
     (2, -2, 2)    95.2543      6.026        11.43        5.26
      (3, 1, 0)    97.0033      6.109        11.19        5.15
     (2, 0, -4)   102.9976      6.384        10.69        4.92
      (3, 1, 2)   108.4189      6.617        21.19        9.75
      (1, 0, 5)   108.9602      6.639        10.60        4.88
      (3, 0, 3)   116.5074      6.936        11.01        5.07
     (2, -3, 1)   120.4651      7.081        22.87       10.53
     (2, 2, -4)   132.3519      7.462        13.70        6.31
      (0, 0, 6)   138.2722      7.622         3.88        1.79
     (2, 1, -5)   140.6857      7.681        32.94       15.16
      (4, 0, 0)   142.6631      7.728         8.67        3.99
     (3, 2, -3)   153.5192      7.940        48.97       22.54
      (3, 1, 4)   153.9051      7.946        49.71       22.88
      (4, 1, 1)   162.8984      8.066        76.17       35.07
      (1, 1, 6)   166.0961      8.097        46.91       21.60
      (4, 0, 2)   171.5398      8.135        77.25       35.56

If you are interested in simulations of powder diffraction patterns look at section Powder diffraction simulations

Using the Gridder classes

xrayutilities provides Gridder classes for 1D, 2D, and 3D data sets. These Gridders map irregular spaced data onto a regular grid. This is often needed after transforming data measured at equally spaced angular positions to reciprocal space were their spacing is irregular.

In 1D this process actually equals the calculation of a histogram. Below you find the most basic way of using the Gridder in 2D. Other dimensions work very similar.

The most easiest use (what most user might need) is

import xrayutilities as xu # import Python package
g = xu.Gridder2D(100, 101) # initialize the Gridder object, which will
# perform Gridding to a regular grid with 100x101 points
#====== load some data here =====
g(x, y, data) # call the gridder with the data
griddata = g.data # the data attribute contains the gridded data.

A more complicated example showing also sequential gridding is shown below. You need sequential gridding when you can not load all data at the same time, which is often problematic with 3D data sets. In such cases you need to specify the data range before the first call to the gridder.

import xrayutilities as xu # import Python package
g = xu.Gridder2D(100, 101) # initialize the Gridder object
g.KeepData(True)
g.dataRange(1, 2, 3, 4)  # (xgrd_min, xgrd_max, ygrd_min, ygrd_max)
#====== load some data here =====
g(x, y, data) # call the gridder with the data
griddata = g.data # the data attribute contains the so far gridded data.

#====== load some more data here =====
g(x, y, data) # call the gridder with the new data
griddata = g.data # the data attribute contains the combined gridded data.

Gridder2D for visualization

Based on the example of parsed data from XRDML files shown above (Reading XRDML files) we show here how to use the Gridder2D class together with matplotlibs contourf.

Si = xu.materials.Si
hxrd = xu.HXRD(Si.Q(1, 1, 0), Si.Q(0, 0, 1))
qx, qy, qz = hxrd.Ang2Q(om, tt)
gridder = xu.Gridder2D(200, 600)
gridder(qy, qz, psd)
INT = xu.maplog(gridder.data.transpose(), 6, 0)
# plot the intensity as contour plot
plt.figure()
cf = plt.contourf(gridder.xaxis, gridder.yaxis, INT, 100, extend='min')
plt.xlabel(r'$Q_{[110]}$ ($\mathrm{\AA^{-1}}$)')
plt.ylabel(r'$Q_{[001]}$ ($\mathrm{\AA^{-1}}$)')
cb = plt.colorbar(cf)
cb.set_label(r"$\log($Int$)$ (cps)")
plt.tight_layout()

The shown script results in the plot of the reciprocal space map shown below.

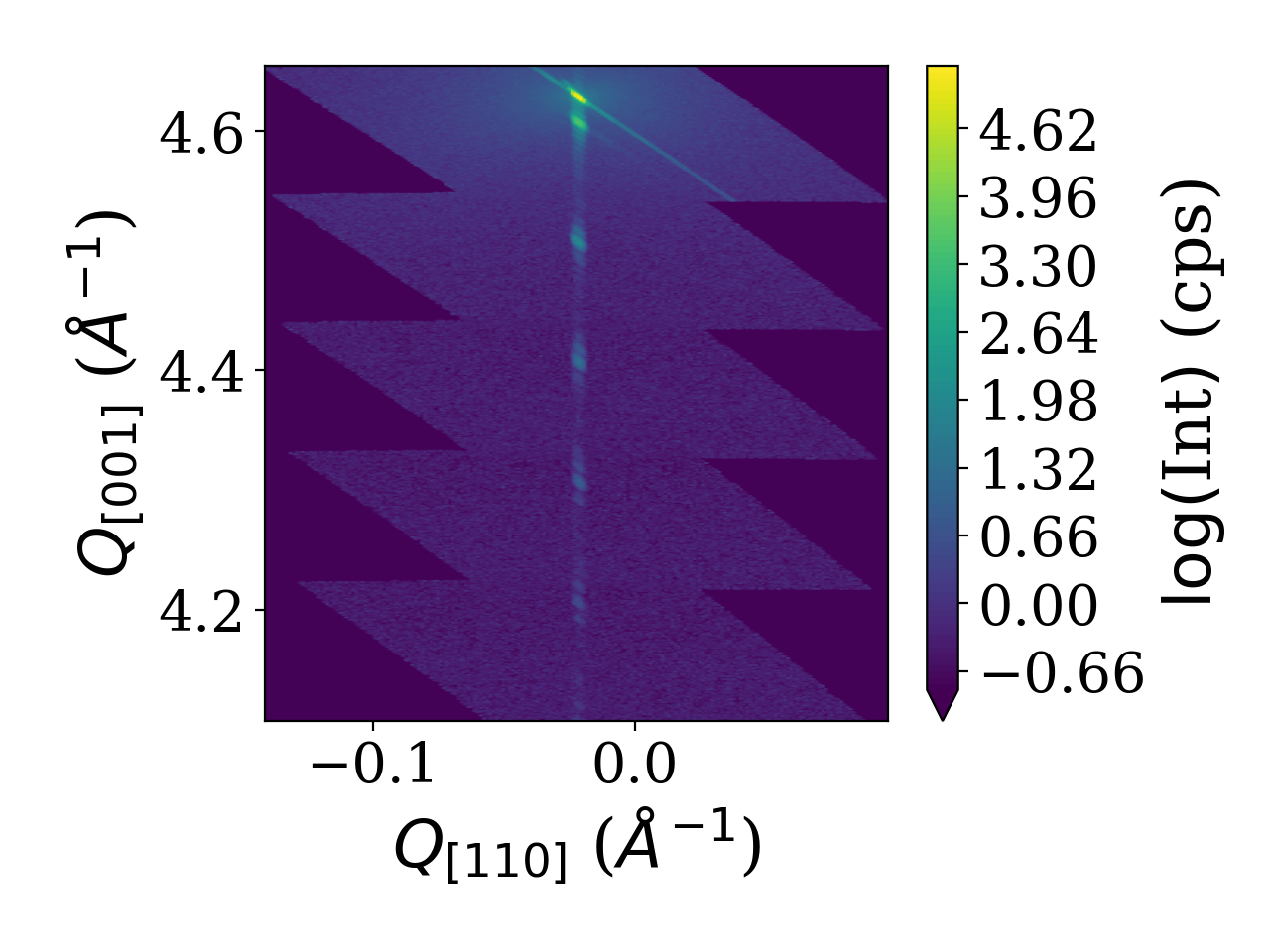
Line cuts from reciprocal space maps

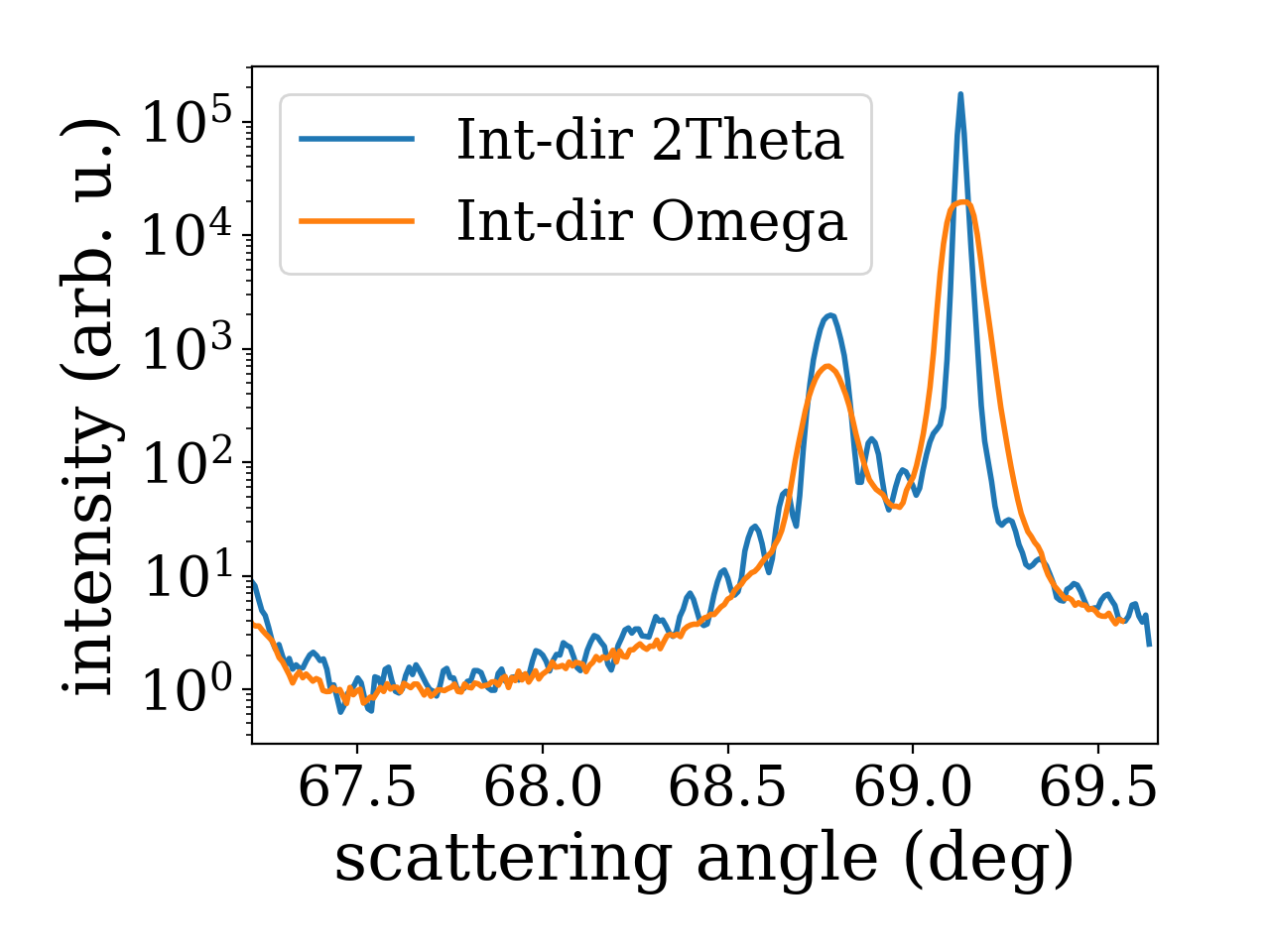
Using the analysis subpackage one can produce line cuts. Starting from the reciprocal space data produced by the reciprocal space conversion as in the last example code we extract radial scan along the crystal truncation rod. For the extraction of line scans the respective functions offer to integrate the data along certain directions. In the present case integration along ‘2Theta’ gives the best result since a broadening in that direction was caused by the beam footprint in the particular experiment. For different line cut functions various integration directions are possible. They are visualized in the figure below.

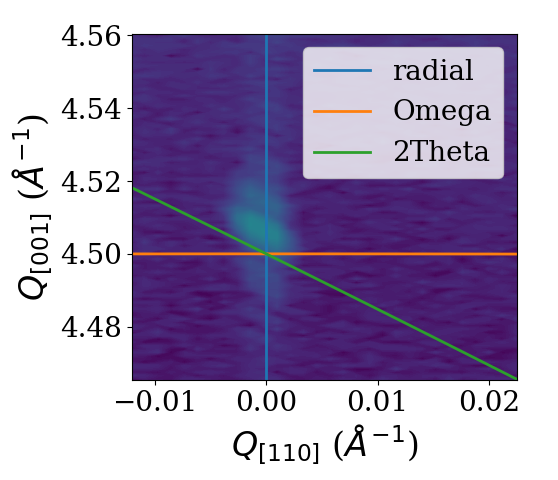
# line cut with integration along 2theta to remove beam footprint broadening
qzc, qzint, cmask = xu.analysis.get_radial_scan([qy, qz], psd, [0, 4.5],
                                                1001, 0.155, intdir='2theta')

# line cut with integration along omega
qzc_om, qzint_om, cmask_om = xu.analysis.get_radial_scan([qy, qz], psd, [0, 4.5],
                                                1001, 0.155, intdir='omega')
plt.figure()
plt.semilogy(qzc, qzint, label='Int-dir 2Theta')
plt.semilogy(qzc_om, qzint_om, label='Int-dir Omega')
plt.xlabel(r'scattering angle (deg)')
plt.ylabel(r'intensity (arb. u.)')
plt.legend()
plt.tight_layout()

See also

the fully working example provided in the examples directory and the other line cut functions in line_cuts

Using the materials subpackage

xrayutilities provides a set of Python classes to describe crystal lattices and materials.

Examples show how to define a new material by defining its lattice and deriving a new material, furthermore materials can be used to calculate the structure factor of a Bragg reflection for an specific energy or the energy dependency of its structure factor for anomalous scattering. Data for this are taken from a database which is included in the download.

First defining a new material from scratch is shown. This is done from the space group and Wyckhoff positions of the atoms inside the unit cell. Depending on the space group number the initialization of a new SGLattice object expects a different amount of parameters. For a cubic materials only the lattice parameter a should be given while for a triclinic materials a, b, c, alpha, beta, and gamma have to be specified. Its similar for the Wyckoff positions. While some Wyckoff positions require only the type of atom others have some free paramters which can be specified. Below we show the definition of zincblende InP as well as for its hexagonal wurtzite polytype together with a quick visualization of the unit cells. A more accurate visualization of the unit cell can be performed when using show_unitcell() with the Mayavi mode or by using the CIF-exporter and an external tool.

import matplotlib.pyplot as plt
import xrayutilities as xu

# elements (which contain their x-ray optical properties) are loaded from
# xrayutilities.materials.elements
In = xu.materials.elements.In
P = xu.materials.elements.P

# define elastic parameters of the material we use a helper function which
# creates the 6x6 tensor needed from the only 3 free parameters of a cubic
# material.
elastictensor = xu.materials.CubicElasticTensor(10.11e+10, 5.61e+10,
                                                4.56e+10)
# definition of zincblende InP:
InP = xu.materials.Crystal(
    "InP", xu.materials.SGLattice(216, 5.8687, atoms=[In, P],
                                  pos=['4a', '4c']),
    elastictensor)

# a hexagonal equivalent which shows how parameters change for material
# definition with a different space group. Since the elasticity tensor is
# optional its not specified here.
InPWZ = xu.materials.Crystal(
    "InP(WZ)", xu.materials.SGLattice(186, 4.1423, 6.8013,
                                      atoms=[In, P], pos=[('2b', 0),
                                                          ('2b', 3/8.)]))
f = plt.figure()
InP.show_unitcell(fig=f, subplot=121)
plt.title('InP zincblende')
InPWZ.show_unitcell(fig=f, subplot=122)
plt.title('InP wurtzite')

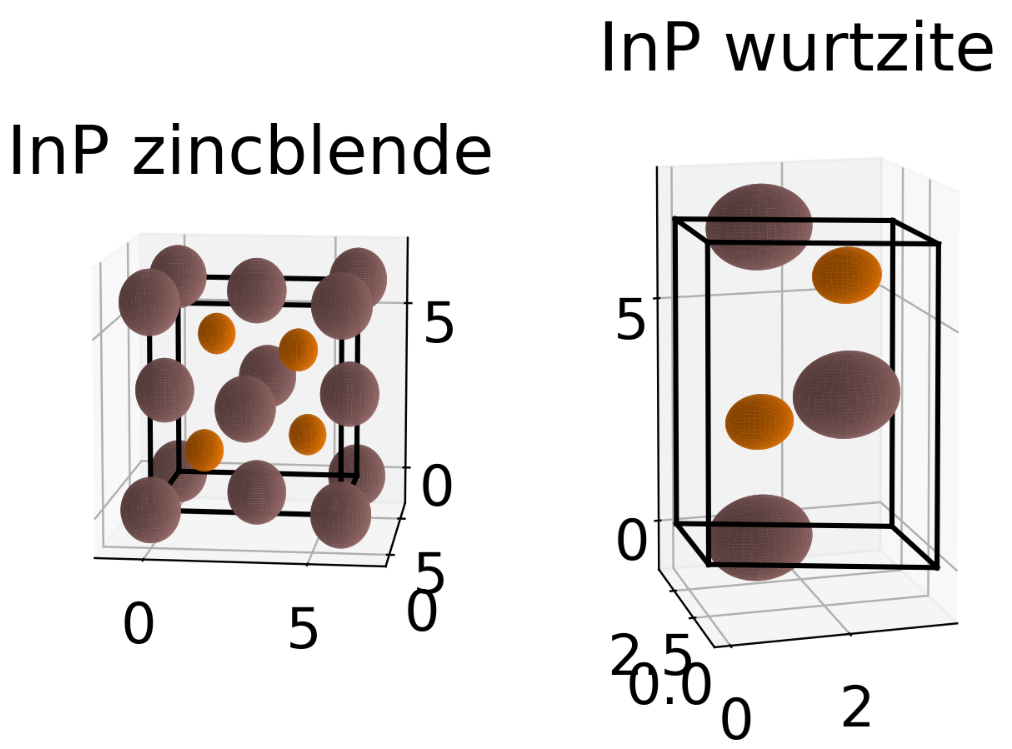
InP (in both variants) is already included in the xu.materials module and can be loaded by

InP = xu.materials.InP
InPWZ = xu.materials.InPWZ

Similar definitions exist for many other materials. Alternatively to giving the Wyckoff labels and parameters one can also specify the position of one atom for every unique site within the unit cell. xrayutilities will then search the corresponding Wyckoff position of this atom and populate therefore populate all equivalent sites as well. For the example of InP in zincblende form the material definition could also look as shown below. Note that instead of the elements also the elemental symbol as string can be used:

InP = xu.materials.Crystal(
    "InP", xu.materials.SGLattice(216, 5.8687, atoms=["In", "P"],
                                  pos=[(0,0,0), (1/4, 1/4, 1/4)]))

Using the material properties the calculation of the reflection strength of a Bragg reflection can be done as follows

import xrayutilities as xu

# defining material and experimental setup
InAs = xu.materials.InAs
energy= 8048 # eV

# calculate the structure factor for InAs (111) (222) (333)
hkllist = [[1, 1, 1], [2, 2, 2], [3, 3, 3]]
for hkl in hkllist:
    qvec = InAs.Q(hkl)
    F = InAs.StructureFactor(qvec, energy)
    print(f"|F| = {abs(F):8.3f}")

Similar also the energy dependence of the structure factor can be determined

import matplotlib.pyplot as plt

energy= numpy.linspace(500, 20000, 5000) # 500 - 20000 eV
F = InAs.StructureFactorForEnergy(InAs.Q(1, 1, 1), energy)

plt.figure(); plt.clf()
plt.plot(energy, F.real, '-k', label='Re(F)')
plt.plot(energy, F.imag, '-r', label='Imag(F)')
plt.xlabel("Energy (eV)"); plt.ylabel("F"); plt.legend()

It is also possible to calculate the components of the structure factor of atoms, which may be needed for input into XRD simulations.

# f = f0(|Q|) + f1(en) + j * f2(en)
import xrayutilities as xu

Fe = xu.materials.elements.Fe # iron atom
Q = [0, 0, 1.9]
en = 10000 # energy in eV

print(f"Iron (Fe): E: {en:9.1f} eV")
print(f"f0: {Fe.f0(xu.math.VecNorm(Q)):8.4g}")
print(f"f1: {Fe.f1(en):8.4g}")
print(f"f2: {Fe.f2(en):8.4g}")

Iron (Fe): E:   10000.0 eV
f0:    21.78
f1:  -0.0178
f2:    2.239

Transformation of SGLattice

SGLattice-objects can be transformed to use a different unit cell setting. This can be used to for example change the origin choice after the material definition or to convert into a totally different setting, e.g. for simulation purposes.

The code below shows the example of the Diamond structure converted between the two different origin choices

import numpy
import xrayutilities as xu
C1 = xu.materials.SGLattice("227:1", 3.5668, atoms=["C"],
                            pos=[(0,0,0)])
C2 = xu.materials.SGLattice("227:2", 3.5668, atoms=["C"],
                            pos=[(1/8, 1/8, 1/8)])
C1 == C2  # False
C3 = C2.transform(numpy.identity(3), (1/8, 1/8, 1/8))
C3 == C1  # True

For dynamical diffraction simulations of cubic crystals with (111) surface it might be required to convert the unit cell in a way that a principle axis is pointing along the surface normal. Using an apropriate conversion matrix this is shown for the example of InP

import xrayutilities as xu
InP111_lattice = xu.materials.InP.lattice.transform(((-1/2, 0, 1),
                                                     (1/2, -1/2, 1),
                                                     (0, 1/2, 1)),
                                                    (0, 0, 0))

While the built in InP uses the cubic setting with space group F-43m(#216) the converted lattice has rhombohedral space group (in this case R3m(#160)) and converted atomic positions.

Visualization of the Bragg peaks in a reciprocal space plane

If you want to explore which peaks are available and reachable in coplanar diffraction geometry and what their relationship between different materials is xrayutilities provides a function which generates a slightly interactive plot which helps you with this task.

import xrayutilities as xu
mat = xu.materials.Crystal('GaTe',
                           xu.materials.SGLattice(194, 4.06, 16.96,
                                                  atoms=['Ga', 'Te'],
                                                  pos=[('4f', 0.17),
                                                       ('4f', 0.602)]))
ttmax = 160
sub = xu.materials.Si
hsub = xu.HXRD(sub.Q(1, 1, -2), sub.Q(1, 1, 1))
ax, h = xu.materials.show_reciprocal_space_plane(sub, hsub, ttmax=160)
hxrd = xu.HXRD(mat.Q(1, 0, 0), mat.Q(0, 0, 1))
ax, h2 = xu.materials.show_reciprocal_space_plane(mat, hxrd, ax=ax)

The generated plot shows all the existing Bragg spots, their (hkl) label is shown when the mouse is over a certain spot and the diffraction angles calculated by the given HXRD object is printed when you click on a certain spot. Not that the primary beam is assumed to come from the left, meaning that high incidence geometry occurs for all peaks with positive inplane momentum transfer.

Calculation of diffraction angles for a general geometry

Often the restricted predefined geometries are not corresponding to the experimental setup, nevertheless xrayutilities is able to calculate the goniometer angles needed to reach a certain reciprocal space position.

For this purpose the goniometer together with the geometric restrictions need to be defined and the q-vector in laboratory reference frame needs to be specified. This works for arbitrary goniometer, however, the user is expected to set up bounds to put restrictions to the number of free angles to obtain reproducible results. In general only three angles are needed to fit an arbitrary q-vector (2 sample + 1 detector angles or 1 sample + 2 detector). More goniometer angles can be kept free if some pseudo-angle constraints are used instead.

The example below shows the necessary code to perform such an angle calculation for a custom defined material with orthorhombic unit cell.

import xrayutilities as xu
import numpy as np

def Pnma(a, b, c):
    # create orthorhombic unit cell with space-group 62,
    # here for simplicity without base
    l = xu.materials.SGLattice(62, a, b, c)
    return l

latticeConstants=[5.600, 7.706, 5.3995]
SmFeO3 = xu.materials.Crystal("SmFeO3", Pnma(*latticeConstants))
# 2S+2D goniometer
qconv=xu.QConversion(('x+', 'z+'), ('z+', 'x+'), (0, 1, 0))
# [1,1,0] surface normal
hxrd = xu.Experiment(SmFeO3.Q(0, 0, 1), SmFeO3.Q(1, 1, 0), qconv=qconv)

hkl=(2, 0, 0)
q_material = SmFeO3.Q(hkl)
q_laboratory = hxrd.Transform(q_material) # transform

print(f"SmFeO3: hkl {hkl}, qvec {np.round(q_material, 5)}")
print(f"Lattice plane distance: {SmFeO3.planeDistance(hkl):.4f}")

#### determine the goniometer angles with the correct geometry restrictions
# tell bounds of angles / (min,max) pair or fixed value for all motors.
# maximum of three free motors! here the first goniometer angle is fixed.
# om, phi, tt, delta
bounds = (5, (-180, 180), (-1, 90), (-1, 90))
ang, qerror, errcode = xu.Q2AngFit(q_laboratory, hxrd, bounds)
print(f"err {errcode} ({qerror:.3g}) angles {np.round(ang, 5)}")
# check that qerror is small!!
print("sanity check with back-transformation (hkl): ",
      np.round(hxrd.Ang2HKL(*ang,mat=SmFeO3),5))

The output of the code above would be similar to:

SmFeO3: hkl (2, 0, 0), qvec [2.24399 0.      0.     ]
Lattice plane distance: 2.8000
err 0 (9.61e-09) angles [ 5.      20.44854 19.65315 25.69328]
sanity check with back-transformation (hkl):  [ 2.  0. -0.]

In the example above all angles can be kept free if a pseudo-angle constraint is used in addition. This is shown below for the incidence angle, which when fixed to 5 degree results in the same goniometer angles as shown above. Currently two helper functions for incidence and exit angles (incidenceAngleConst() and exitAngleConst()) are implemented, but user-defined functions can be supplied.

aiconstraint = xu.q2ang_fit.incidenceAngleConst
bounds = ((0, 90), (-180, 180), (-1, 90), (-1, 90))
ang, qerror, errcode = xu.Q2AngFit(
    q_laboratory, hxrd, bounds,
    constraints=[{'type':'eq', 'fun': lambda a: aiconstraint(a, 5, hxrd)}, ])

User-specific config file

Several options of xrayutilities can be changed by options in a config file. This includes the default x-ray energy as well as parameters to set the number of threads used by the parallel code and the verbosity of the output.

The default options are stored inside the installad Python module and should not be changed. Instead it is suggested to use a user-specific config file ‘~/.xrayutilities.conf’ or a ‘xrayutilities.conf’ file in the working directory.

An example of such a user config file is shown below:

# begin of xrayutilities configuration
[xrayutilities]

# verbosity level of information and debugging outputs
#   0: no output
#   1: very import notes for users
#   2: less import notes for users (e.g. intermediate results)
#   3: debuging output (e.g. print everything, which could be interesing)
#   levels can be changed in the config file as well
verbosity = 1

# default wavelength in angstrom,
wavelength = MoKa1 # Molybdenum K alpha1 radiation (17479.374eV)

# default energy in eV
# if energy is given wavelength settings will be ignored
#energy = 10000 #eV

# number of threads to use in parallel sections of the code
nthreads = 1
#   0: the maximum number of available threads will be used (as returned by
#      omp_get_max_threads())
#   n: n-threads will be used

Determining detector parameters

In the following three examples of how to determine the detector parameters for linear and area detectors is given. The procedure we use is in more detail described in this article.

Linear detectors

To determine the detector parameters of a linear detector one needs to perform a scan with the detector angle through the primary beam and aquire a detector spectrum at any point.

Using the following script determines the parameters necessary for the detector initialization, which are:

• pixelwidth of one channel

• the center channel

• and the detector tilt (optional)

"""
example script to show how the detector parameters
such as pixel width, center channel and detector tilt
can be determined for a linear detector.
"""

import os

import xrayutilities as xu

# load any data file with with the detector spectra of a reference scan
# in the primary beam, here I use spectra measured with a Seifert XRD
# diffractometer
dfile = os.path.join("data", "primarybeam_alignment20130403_2_dis350.nja")
s = xu.io.SeifertScan(dfile)

ang = s.axispos["T"]  # detector angles during the scan
spectra = s.data[:, :, 1]  # detector spectra aquired

# determine detector parameters
# this function accepts some optional arguments to describe the goniometer
# see the API documentation
pwidth, cch, tilt = xu.analysis.linear_detector_calib(ang, spectra,
                                                      usetilt=True)

Area detector (Variant 1)

To determine the detector parameters of a area detector one needs to perform scans with the detector angles through the primary beam and aquire a detector images at any position. For the area detector at least two scans (one with the outer detector and and one with the inner detector angle) are required.

Using the following script determines the parameters necessary for the detector initialization from such scans in the primary beam only. Further down we discuss an other variant which is also able to use additionally detector images recorded at the Bragg reflection of a known reference crystal.

The determined detector parameters are:

• center channels: position of the primary beam at the true zero position of the goniometer (considering the outer angle offset) (2 parameters)

• pixelwidth of the channels in both directions (2 parameters), these two parameters can be replaced by the detector distance (1 parameter) if the pixel size is given as an input

• detector tilt azimuth in degree from 0 to 360

• detector tilt angle in degree (>0deg)

• detector rotation around the primary beam in degree

• outer angle offset, which describes a offset of the outer detector angle from its true zero position

The misalignment parameters as well as the pixel size can be fixed during the fitting.

"""
example script to show the detector parameter determination for area detectors
from images recorded in the primary beam
"""

import os

import xrayutilities as xu

en = 10300.0  # eV
datadir = os.path.join("data", "wire_")  # data path for CCD files
# template for the CCD file names
filetmp = os.path.join(datadir, "wire_12_%05d.edf.gz")

# manually selected images
# select images which have the primary beam fully on the CCD
imagenrs = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
            20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]

images = []
ang1 = []
ang2 = []

# read images and angular positions from the data file
# this might differ for data taken at different beamlines since
# they way how motor positions are stored is not always consistent
for imgnr in imagenrs:
    filename = filetmp % imgnr
    edf = xu.io.EDFFile(filename)
    images.append(edf.data)
    ang1.append(float(edf.header['ESRF_ID01_PSIC_NANO_NU']))
    ang2.append(float(edf.header['ESRF_ID01_PSIC_NANO_DEL']))


# call the fit for the detector parameters
# detector arm rotations and primary beam direction need to be given.
# in total 9 parameters are fitted, however the severl of them can
# be fixed. These are the detector tilt azimuth, the detector tilt angle, the
# detector rotation around the primary beam and the outer angle offset
# The detector pixel size or the detector distance should be kept unfixed to
# be optimized by the fit.
param, eps = xu.analysis.sample_align.area_detector_calib(
    ang1, ang2, images, ['z+', 'y-'], 'x+',
    start=(None, None, 1.0, 45, 0, -0.7, 0),
    fix=(False, False, True, False, False, False, False),
    wl=xu.en2lam(en))

A possible output of this script could be

fitted parameters: epsilon: 8.0712e-08 (2,[‘Parameter convergence’]) param: (cch1,cch2,pwidth1,pwidth2,tiltazimuth,tilt,detrot,outerangle_offset) param: 140.07 998.34 4.4545e-05 4.4996e-05 72.0 1.97 -0.792 -1.543 please check the resulting data (consider setting plot=True) detector rotation axis / primary beam direction (given by user): [‘z+’, ‘y-’] / x+ detector pixel directions / distance: z- y+ / 1 detector initialization with: init_area(‘z-’, ‘y+’, cch1=140.07, cch2=998.34, Nch1=516, Nch2=516, pwidth1=4.4545e-05, pwidth2=4.4996e-05, distance=1., detrot=-0.792, tiltazimuth=72.0, tilt=1.543) AND ALWAYS USE an (additional) OFFSET of -1.9741deg in the OUTER DETECTOR ANGLE!

The output gives the fitted detector parameters and compiles the Python code line one needs to use to initialize the detector. Important to note is that the outer angle offset which was determined by the fit (-1.9741 degree in the aboves example) is not included in the initialization of the detector parameters but needs to be used in every call to the q-conversion function as offset. This step needs to be performed manually by the user!

Area detector (Variant 2)

In addition to scans in the primary beam this variant enables also the use of detector images recorded in scans at Bragg reflections of a known reference materials. However this also required that the sample orientation and x-ray wavelength need to be fit. To keep the additional parameters as small as possible we only implemented this for symmetric coplanar diffractions.

The advantage of this method is that it is more sensitive to the outer angle offset also at large detector distances. The additional parameters are:

• sample tilt angle in degree

• sample tilt azimuth in degree

• and the x-ray wavelength in angstrom

"""
example script to show the detector parameter determination for area detectors
from images recorded in the primary beam and at known symmetric coplanar Bragg
reflections of a reference crystal
"""

import os

import numpy
import xrayutilities as xu

Si = xu.materials.Si

datadir = 'data'
specfile = "si_align.spec"

en = 15000  # eV
wl = xu.en2lam(en)
imgdir = os.path.join(datadir, "si_align_")  # data path for CCD files
filetmp = "si_align_12_%04d.edf.gz"

qconv = xu.QConversion(['z+', 'y-'], ['z+', 'y-'], [1, 0, 0])
hxrd = xu.HXRD(Si.Q(1, 1, -2), Si.Q(1, 1, 1), wl=wl, qconv=qconv)

# manually selected images

s = xu.io.SPECFile(specfile, path=datadir)
imagenrs = []
for num in [61, 62, 63, 20, 21, 26, 27, 28]:
    s[num].ReadData()
    imagenrs = numpy.append(imagenrs, s[num].data['ccd_n'])

# avoid images which do not have to full beam on the detector as well as
# other which show signal due to cosmic radiation
avoid_images = [37, 57, 62, 63, 65, 87, 99, 106, 110, 111, 126, 130, 175,
                181, 183, 185, 204, 206, 207, 208, 211, 212, 233, 237, 261,
                275, 290]

images = []
ang1 = []  # outer detector angle
ang2 = []  # inner detector angle
sang = []  # sample rocking angle
hkls = []  # Miller indices of the reference reflections


def hotpixelkill(ccd):
    """
    function to remove hot pixels from CCD frames
    ADD REMOVE VALUES IF NEEDED!
    """
    ccd[304, 97] = 0
    ccd[303, 96] = 0
    return ccd


# read images and angular positions from the data file
# this might differ for data taken at different beamlines since
# they way how motor positions are stored is not always consistent
for imgnr in numpy.sort(list(set(imagenrs) - set(avoid_images))[::4]):
    filename = os.path.join(imgdir, filetmp % imgnr)
    edf = xu.io.EDFFile(filename)
    ccd = hotpixelkill(edf.data)
    images.append(ccd)
    ang1.append(float(edf.header['motor_pos'].split()[4]))
    ang2.append(float(edf.header['motor_pos'].split()[3]))
    sang.append(float(edf.header['motor_pos'].split()[1]))
    if imgnr > 1293.:
        hkls.append((0, 0, 0))
    elif imgnr < 139:
        hkls.append((0, 0, numpy.sqrt(27)))  # (3,3,3))
    else:
        hkls.append((0, 0, numpy.sqrt(75)))  # (5,5,5))

# call the fit for the detector parameters.
# Detector arm rotations and primary beam direction need to be given
# in total 8 detector parameters + 2 additional parameters for the reference
# crystal orientation and the wavelength are fitted, however the 4 misalignment
# parameters of the detector and the 3 other parameters can be fixed.
# The fixable parameters are detector tilt azimuth, the detector tilt angle,
# the detector rotation around the primary beam, the outer angle offset, sample
# tilt, sample tilt azimuth and the x-ray wavelength
# Additionally if accurately known the detector pixel size can be given and
# fixed and instead the detector distance can be fitted.
param, eps = xu.analysis.area_detector_calib_hkl(
    sang, ang1, ang2, images, hkls, hxrd, Si, ['z+', 'y-'], 'x+',
    start=(None, None, 1.0, 45, 1.69, -0.55, -1.0, 1.3, 60., wl),
    fix=(False, False, True, False, False, False, False, False, False, False),
    plot=True)

# Following is an example of the output of the summary of the
# area_detector_calib_hkl function
# total time needed for fit: 624.51sec
# fitted parameters: epsilon: 9.9159e-08 (2,['Parameter convergence'])
# param:
# (cch1,cch2,pwidth1,pwidth2,tiltazimuth,tilt,detrot,outerangle_offset,
# sampletilt,stazimuth,wavelength)
# param: 367.12 349.27 6.8187e-05 6.8405e-05 131.4 2.87 -0.390 -0.061 1.201
# 318.44 0.8254
# please check the resulting data (consider setting plot=True)
# detector rotation axis / primary beam direction (given by user): ['z+', 'y-']
# / x+
# detector pixel directions / distance: z- y+ / 1
#   detector initialization with:
#   init_area('z-', 'y+', cch1=367.12, cch2=349.27, Nch1=516, Nch2=516,
#   pwidth1=6.8187e-05, pwidth2=6.8405e-05, distance=1., detrot=-0.390,
#   tiltazimuth=131.4, tilt=2.867)
# AND ALWAYS USE an (additional) OFFSET of -0.0611deg in the OUTER
# DETECTOR ANGLE!