Simulation examples

In the following a few code-snippets are shown which should help you getting started with reflectivity and diffraction simulations using xrayutilities. All simulations in xrayutilities are for layers systems and currently there are no plans to extend this to other geometries. Note that not all of the codes shown in the following will be run-able as stand-alone scripts. For fully running scripts look in the examples directory in the download.

Building Layer stacks for simulations

The basis of all simulations in xrayutilities are stacks of layers. Therefore several functions exist to build up such layered systems. The basic building block of all of them is a Layer object which takes a material and its thickness in ångström as initializing parameter.

import xrayutilities as xu
lay = xu.simpack.Layer(xu.materials.Si, 200)

In the shown example a silicon layer with 20 nm thickness is created. The first argument is the material of the layer. For diffraction simulations this needs to be derived from the Crystal-class. This means all predefined materials in xrayutitities can be used for this purpose. For x-ray reflectivity simulations, however, also knowing the chemical composition and density of the material is sufficient.

A 5 nm thick metallic CoFe compound layer can therefore be defined sublayers

rho_cf = 0.5*8900 + 0.5*7874  # mass density in kg/m^3
mCoFe = xu.materials.Amorphous('CoFe', rho_cf)
lCoFe = xu.simpack.Layer(mCoFe, 50)

Note

The Layer object can have several more model dependent properties discussed in detail below.

When several layers are defined they can be combined to a LayerStack which is used for the simulations below.

sub = xu.simpack.Layer(xu.materials.Si, float('inf'))
lay1 = xu.simpack.Layer(xu.materials.Ge, 200)
lay2 = xu.simpack.Layer(xu.materials.SiO2, 30)
ls = xu.simpack.LayerStack('Si/Ge', sub, lay1, lay2)
# or equivalently
ls = xu.simpack.LayerStack('Si/Ge', sub + lay1 + lay2)

The last two lines show two different options of creating a stack of layers. As is shown in the last example the substrate thickness can be infinite (see below) and layers can be also stacked by summation. For creation of more complicated superlattice stacks one can further use multiplication

lay1 = xu.simpack.Layer(xu.materials.SiGe(0.3), 50)
lay2 = xu.simpack.Layer(xu.materials.SiGe(0.6), 40)
layerstack = xu.simpack.LayerStack('Si/SiGe SL', sub + 5*(lay1 + lay2))

Pseudomorphic Layers

All stacks of layers described above use the materials in the layer as they are supplied. However, epitaxial systems often adopt the inplane lattice parameter of the layers beneath. To mimic this behavior you can either supply the Layer objects which custom Crystal objects which have the appropriate lattice parameters or use the PseudomorphicStack* classes which to the adaption of the lattice parameters automatically. In this respect the ‘relaxation’ parameter of the Layer class is important since it allows to create partially/fully relaxed layers.

sub = xu.simpack.Layer(xu.materials.Si, float('inf'))
buf1 = xu.simpack.Layer(xu.materials.SiGe(0.5), 5000, relaxation=1.0)
buf2 = xu.simpack.Layer(xu.materials.SiGe(0.8), 5000, relaxation=1.0)
lay1 = xu.simpack.Layer(xu.materials.SiGe(0.6), 50, relaxation=0.0)
lay2 = xu.simpack.Layer(xu.materials.SiGe(1.0), 50, relaxation=0.0)
# create pseudomorphic superlattice stack
pls = xu.simpack.PseudomorphicStack001('SL 5/5', sub+buf1+buf2+5*(lay1+lay2))

Note

As indicated by the function name the PseudomorphicStack currently only works for (001) surfaces and cubic materials. Implementations for other surface orientations are planned.

If you would like to check the resulting lattice objects of the different layers you could use:

for l in pls:
    print(l.material.lattice)

Special layer types

So far one special layer mimicking a layer with gradually changing chemical composition is implemented. It consists of several thin sublayers of constant composition. So in order to obtain a smooth grading one has to select enough sublayers. This however has a negativ impact on the performance of all simulation models. A tradeoff needs to found! Below a graded SiGe buffer is shown which consists of 100 sublayers and has total thickness of 1 µm.

buf = xu.simpack.GradedLayerStack(xu.materials.SiGe,
                                  0.2,  # xfrom Si0.8Ge0.2
                                  0.7,  # xto Si0.3Ge0.7
                                  100,  # number of sublayers
                                  10000,  # total thickness
                                  relaxation=1.0)

Setting up a model

This sectiondescribes the parameters which are common for all diffraction models in xrayutilties-simpack. All models need a list of Layers for which the reflected/diffracted signal will be calculated. Further all models have some common parameters which allow scaling and background addition in the model output and contain general information about the calculation which are model-independent. These are

• ‘experiment’: an Experiment/HXRD object which defines the surface geometry of the model. If none is given a default class with (001) surface is generated.

• ‘resolution_width’: width of the Gaussian resolution function used to convolute with the data. The unit of this parameters depends on the model and can be either in degree or 1/AA.

• ‘I0’: is the primary beam flux/intensity

• ‘background’: is the background added to the simulation after it was scaled by I0

• ‘energy’: energy in eV used to obtain the optical parameters for the simulation. The energy can alternatively also be supplied via the ‘experiment’ parameter, however, the ‘energy’ value overrules this setting. If no energy is given the default energy from the configuration is used.

The mentioned parameters can be supplied to the constructor method of all model classes derived from LayerModel, which applies to all examples mentioned below.

m = xu.simpack.SpecularReflectivityModel(layerstack, I0=1e6, background=1,
                                         resolution_width=0.001)

Reflectivity calculation and fitting

This section shows the calculation and fitting of specular x-ray reflectivity curves as well as the calculation of diffuse x-ray reflectivity curves/maps.

Specular x-ray reflectivity

For the specular reflectivity models currently only the Parrat formalism including non-correlated roughnesses is implemented. A minimal working example for a reflectivity calculation follows.

import numpy
# building a stack of layers
sub = xu.simpack.Layer(xu.materials.GaAs, float('inf'), roughness=2.0)
lay1 = xu.simpack.Layer(xu.materials.AlGaAs(0.25), 75, roughness=2.5)
lay2 = xu.simpack.Layer(xu.materials.AlGaAs(0.75), 25, roughness=3.0)
pls = xu.simpack.PseudomorphicStack001('pseudo', sub+5*(lay1+lay2))

# reflectivity calculation
m = xu.simpack.SpecularReflectivityModel(pls, sample_width=5, beam_width=0.3)
ai = numpy.linspace(0, 5, 10000)
Ixrr = m.simulate(ai)

In addition to the layer thickness also the roughness and density (in kg/m^3) of a Layer can be set since they are important for the reflectivity calculation. This can be done upon definition of the Layer or also manipulated at any later stage. Such x-ray reflectivity calculations can also be fitted to experimental data using the FitModel class which is shown in detail in the example below (which is also included in the example directory). The fitting is performed using the lmfit Python package which needs to be installed when you want to use this fitting function. This package allows to build complicated models including bounds and correlations between parameters.

import lmfit
import numpy

import xrayutilities as xu

# load experimental data
ai, edata, eps = numpy.loadtxt('data/xrr_data.txt'), unpack=True)
ai /= 2.0

# define layers
# SiO2 / Ru(5) / CoFe(3) / IrMn(3) / AlOx(10)
lSiO2 = xu.simpack.Layer(xu.materials.SiO2, numpy.inf, roughness=2.5)
lRu = xu.simpack.Layer(xu.materials.Ru, 47, roughness=2.8)
rho_cf = 0.5*8900 + 0.5*7874
mat_cf = xu.materials.Amorphous('CoFe', rho_cf)
lCoFe = xu.simpack.Layer(mat_cf, 27, roughness=4.6)
lIrMn = xu.simpack.Layer(xu.materials.Ir20Mn80, 21, roughness=3.0)
lAl2O3 = xu.simpack.Layer(xu.materials.Al2O3, 100, roughness=5.5)

# create model
m = xu.simpack.SpecularReflectivityModel(lSiO2, lRu, lCoFe, lIrMn, lAl2O3,
                                         energy='CuKa1', resolution_width=0.02,
                                         sample_width=6, beam_width=0.25,
                                         background=81, I0=6.35e9)

# embed model in fit code
fitm = xu.simpack.FitModel(m, plot=True, verbose=True)

# set some parameter limitations
fitm.set_param_hint('SiO2_density', vary=False)
fitm.set_param_hint('Al2O3_density', min=0.8*xu.materials.Al2O3.density,
                    max=1.2*xu.materials.Al2O3.density)
p = fitm.make_params()
fitm.set_fit_limits(xmin=0.05, xmax=8.0)

# perform the fit
res = fitm.fit(edata, p, ai, weights=1/eps)
lmfit.report_fit(res, min_correl=0.5)
# export the fit result for the full data range (Note that only data between
# xmin and xmax were actually optimized)
numpy.savetxt(
    "xrrfit.dat",
    numpy.vstack((ai, res.eval(res.params, x=ai))).T,
    header="incidence angle (deg), fitted intensity (arb. u.)",
)

This script can interactively show the fitting progress and after the fitting shows the final plot including the x-ray reflectivity trace of the initial and final parameters.

The picture shows the final plot of the fitting example shown in one of the example scripts.

After building a SpecularReflectivityModel is built or fitted the density profile resulting from the thickness and roughness of layers can be plotted easily by

m.densityprofile(500, plot=True)  # 500 number of points

Diffuse reflectivity calculations

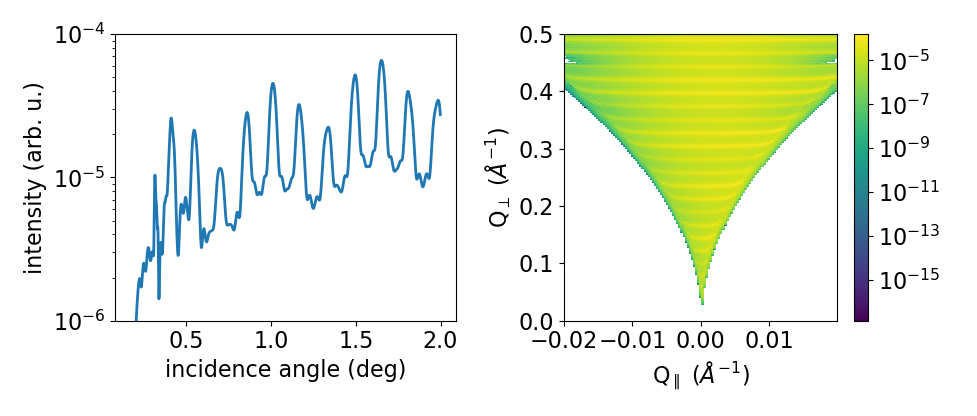
For the calculation of diffuse x-ray reflectivity the LayerStack is built equally as shown before. The only difference is that an additional parameter for the lateral correlation length of the roughness can be included: lat_correl. The DiffuseReflectivityModel also takes special parameters which change the vertical correlection length and the way how the diffuse reflectivity is calculated (to be document in more detail). For a Si/Ge superlattice with 5 periods the calculation of the diffuse reflectivity signal at the specular rod is calculated using the simulate() method. A map of the diffuse reflectivity which can be obtained in the coplanar reflection plane can be calculated with the simulate_map() method.

from matplotlib.pylab import *
import xrayutilities as xu
sub = xu.simpack.Layer(xu.materials.Si, inf, roughness=1, lat_correl=100)
lay1 = xu.simpack.Layer(xu.materials.Si, 200, roughness=1, lat_correl=200)
lay2 = xu.simpack.Layer(xu.materials.Ge, 70, roughness=3, lat_correl=50)
ls = xu.simpack.LayerStack('SL 5', sub+5*(lay2+lay1))

alphai = arange(0.17, 2, 0.001)  # for the calculation on the specular rod
qz = arange(0, 0.5, 0.0005)  # for the map calculation
qL = arange(-0.02, 0.02, 0.0003)

m = xu.simpack.DiffuseReflectivityModel(ls, sample_width=10, beam_width=1,
                                        energy='CuKa1', vert_correl=1000,
                                        vert_nu=0, H=1, method=2, vert_int=0)
d = m.simulate(alphai)
imap = m.simulate_map(qL, qz)

figure()
subplot(121)
semilogy(alphai, d, label='diffuse XRR')
xlabel('incidence angle (deg)')
ylabel('intensity (arb. u.)')
ylim(1e-6, 1e-4)

subplot(122)
pcolor(qL, qz, imap.T, norm=mpl.colors.LogNorm())
xlabel(r'Q$_\parallel$ ($\mathrm{\AA^{-1}}$)')
ylabel(r'Q$_\perp$ ($\mathrm{\AA^{-1}}$)')
colorbar()
tight_layout()

The resulting figure shows the simulation result. Currently you have to refer to the docstrings and implementation for further details.

Diffraction calculation

From the very same models as used for XRR calculation one can also perform crystal truncation rod simulations around certain Bragg peaks using various different diffraction models. Depending on the system to model you will have to choose the most apropriate model. Below a short description of the implemented models is given followed by two examples.

Kinematical diffraction models

The most basic models consider only the kinematic diffraction of layers and substrate. Especially the semiinfinite substrate is not well described using the kinematical approximation which results in considerable deviations in close vicinity to substrate Bragg peak with respect to the more acurate dynamical diffraction models.

Such a basic model is employed by

en = 9000  # eV
mk = xu.simpack.KinematicalModel(pls, energy=en, resolution_width=0.0001)
Ikin = mk.simulate(qz, hkl=(0, 0, 4))

A more appealing kinematical model is represented by the KinematicalMultiBeamModel class which implements a true multibeam theory is, however, restricted to the use of (001) surfaces and layer thicknesses will be changed to be a multiple of the out of plane lattice spacing. This is necessary since otherwise the structure factor of the unit cell can not be used for the calculation.

It can be employed by

mk = xu.simpack.KinematicalMultiBeamModel(pls, energy=en,
                                          surface_hkl=(0, 0, 1),
                                          resolution_width=0.0001)
Imult = mk.simulate(qz, hkl=(0, 0, 4))

This model is expected to provide good results especially far away from the substrate peak where the influence of other Bragg peaks on the truncation rod and the variation of the structure factor can not be neglected.

Both kinematical model’s simulate() method offers two keyword arguments with which basic absorption and refraction correction can be added to the basic models.

Note

The kinematical models can also handle a semi-infinitely thick substrate which results in a diverging intensity at the Bragg peak but provides a basic description of the substrates truncation rod.

Dynamical diffraction models

Acurate description of the diffraction from thin films in close vicinity to the diffraction signal from a bulk substrate is only possible using the dynamical diffraction theory. In xrayutilities the dynamical two-beam theory with 4 tiepoints for the calculation of the dispersion surface is implemented. To use this theory you have to supply the simulate() method with the incidence angle in degree. Accordingly the ‘resolution_width’ parameter is also in degree for this model.

resol = 0.001  # resolution in incidence angle
md = xu.simpack.DynamicalModel(pls, energy=en, resolution_width=resol)
Idyn = md.simulate(ai, hkl=(0, 0, 4))

A second simplified dynamical model (SimpleDynamicalCoplanarModel) is also implemented should, however, not be used since its approximations cause mistakes in almost all relevant cases.

The DynamicalModel supports the calculation of diffracted signal for ‘S’ and ‘P’ polarization geometry. To simulate diffraction data of laboratory sources with Ge(220) monochromator crystal one should use:

.. testcode::

import math qGe220 = linalg.norm(xu.materials.Ge.Q(2, 2, 0)) thMono = math.asin(qGe220 * xu.config.WAVELENGTH / (4*math.pi)) md = xu.simpack.DynamicalModel(pls,

Cmono=math.cos(2 * thMono), polarization=’both’)

Idyn = md.simulate(ai, hkl=(0, 0, 4))

Comparison of diffraction models

Below we show the different implemented models for the case of epitaxial GaAs/AlGaAs and Si/SiGe bilayers. These two cases have very different separation of the layer Bragg peak from the substrate and therefore provide good model system for our models.

We will compare the (004) Bragg peak calculated with different models and but otherwise equal parameters. For scripts used to perform the shown calculation you are referred to the examples directory.

XRD simulations of the (004) Bragg peak of ~100 nm AlGaAs on GaAs(001) using various diffraction models

XRD simulations of the (004) Bragg peak of 15 nm Si_0.4 Ge_0.6 on Si(001) using various diffraction models

As can be seen in the images we find that for the AlGaAs system all models except the very basic kinematical model yield an very similar diffraction signal. The second kinematic diffraction model considering the contribution of multiple Bragg peaks on the same truncation rod fails to describe only the ratio of substrate and layer signal, but otherwise results in a very similar line shape as the traces obtained by the dynamic theory.

For the SiGe/Si bilayer system bigger differences between the kinematic and dynamic models are found. Further also the difference between the simpler and more sophisticated dynamic model gets obvious further away from the reference position. Interestingly also the multibeam kinematic theory differs considerable from the best dynamic model. As is evident from this second comparison the correct choice of model for the particular system under condideration is crucial for comparison with experimental data.

Fitting of diffraction data

All diffraction models can be embedded into the FitModel class, which is suitable to refine the model parameters. Below (and in the examples directory) a runnable script is shown which shows the fitting for a pseudomorphic InMnAs epilayer on InAs(001). The fitting is performed using the lmfit Python package which needs to be installed when you want to use this fitting function. As one can see below the set_param_hint() function can be used to set up the respective fit parameters including their boundaries and possible correlation with other parameters of the model. It should be equally possible to fit more complex layer structures, however, I expect that one needs to adjust manually the starting parameters to yield something very reasonable. Since this capabilities are rather new please report back any success/problems you have with this via the mailing list.

from copy import deepcopy
import xrayutilities as xu
from matplotlib.pylab import *

# global parameters
wavelength = xu.wavelength('CuKa1')
offset = -0.035  # angular offset of the zero position of the data

# set up LayerStack for simulation: InAs(001)/(In,Mn)As(~25 nm)
InAs = deepcopy(xu.materials.InAs)  # do not modify internal database
InAs.a = 6.057
lInAs = xu.simpack.Layer(InAs, inf)
InMnAs = xu.materials.Crystal('InMnAs', xu.materials.SGLattice(
    216, 6.050, atoms=('In', 'Mn', 'As'), pos=('4a', '4a', '4c'),
    occ=(0.99, 0.01, 1)), cij=InAs.cij)
lInMnAs = xu.simpack.Layer(InMnAs, 254, relaxation=0)
pstack = xu.simpack.PseudomorphicStack001('list', lInAs, lInMnAs)

# set up simulation object
thetaMono = arcsin(wavelength/(2 * xu.materials.Ge.planeDistance(2, 2, 0)))
Cmono = cos(2 * thetaMono)
dyn = xu.simpack.DynamicalModel(pstack, I0=1.5e9, background=0,
                                resolution_width=2e-3, polarization='both',
                                Cmono=Cmono)
fitmdyn = xu.simpack.FitModel(dyn)
fitmdyn.set_param_hint('InMnAs_c', vary=True, min=6.02, max= 6.06)
fitmdyn.set_param_hint('InAs_a', vary=True)
fitmdyn.set_param_hint('InMnAs_a', expr='InAs_a')
fitmdyn.set_param_hint('resolution_width', vary=True)
params = fitmdyn.make_params()

# plot experimental data
f = figure(figsize=(7,5))
d = xu.io.RASFile('inas_layer_radial_002_004.ras.bz2', path='examples/data')
scan = d.scans[-1]
tt = scan.data[scan.scan_axis] - offset
semilogy(tt, scan.data['int'], 'o-', ms=3, label='data')

# perform fit and plot the result
fitmdyn.lmodel.set_hkl((0, 0, 4))
ai = (d.scans[-1].data[d.scan.scan_axis] - offset)/2
fitr = fitmdyn.fit(d.scans[-1].data['int'], params, ai)
# print(fitr.fit_report())  # to get a summary of the fitted parameters

The resulting figure shows reasonable agreement between the dynamic diffraction simulation and the experimental data.

Powder diffraction simulations

Powder diffraction patterns can be calculated using PowderModel. A specialized class for the definition of powdered materials named Powder exists. The class constructor takes the materials volume and several material parameters specific for the powder material. Among them are crystallite_size_gauss and strain_gauss which can be used to include the effect of finite crystallite size and microstrain. Texture modelled by the March-Dollase pole density offers the preferred_orientation direction parameter as well as a preferred_orientation_factor variable.

The PowderModel internally uses PowderDiffraction for its calculations which is based on the fundamental parameters approach. The fundamental parameters approach code used here can was originally implemented and documented here: http://dx.doi.org/10.6028/jres. 120.014.c and http://dx.doi.org/10.6028/jres.120.014.

Several setup specific parameters should be adjusted by a user-specific configuration file or by supplying the appropriate parameters using the fpsettings argument of PowderModel.

If the correct settings are included in the config file the powder diffraction signal of a mixed sample of Co and Fe can be calculated with

import numpy
import xrayutilities as xu

tt = numpy.arange(5, 120, 0.01)
Fe_powder = xu.simpack.Powder(xu.materials.Fe, 1,
                              crystallite_size_gauss=100e-9)
Co_powder = xu.simpack.Powder(xu.materials.Co, 5,  # 5 times more Co
                              crystallite_size_gauss=200e-9)
pm = xu.simpack.PowderModel(Fe_powder, Co_powder, I0=100)
inte = pm.simulate(tt)
pm.close()  # after end-of-use

Note that in MS windows and macOS you need to encapsulate this code into a dummy function to allow for the multiprocessing module to work correctly. See the Python documentation for details. The code then must look like:

import numpy
import xrayutilities as xu
from multiprocessing import freeze_support

def main():
    tt = numpy.arange(5, 120, 0.01)
    Fe_powder = xu.simpack.Powder(xu.materials.Fe, 1,
                                  crystallite_size_gauss=100e-9)
    Co_powder = xu.simpack.Powder(xu.materials.Co, 5,  # 5 times more Co
                                  crystallite_size_gauss=200e-9)
    pm = xu.simpack.PowderModel(Fe_powder, Co_powder, I0=100)
    inte = pm.simulate(tt)
    pm.close()

if __name__ == '__main__':
    freeze_support()  # only required on MS Windows
    main()